报告题目:On linear preservers between matrices over an arbitrary field

报告人:黄毅青 教授 台湾中山大学

邀请人:刘 磊

报告时间:2023年11月10日(周五)下午14:30-15：30

报告地点：腾讯会议598-998-219

报告人简介：黄毅青 (Ngai-Ching Wong) ，台湾中山大学教授。黄毅青在泛函分析、算子代数领域开展了卓有成效的研究工作，获得了丰硕的研究成果。2004年，黄毅青教收受华人数学家大会 ICCM 2004邀请做45分钟报告。黄毅青教授发表SCI论文一百多篇，同时在多份著名SCI数学期刊，如Operators and Matrices, Linear and Multilinear Algebra, Banach Journal of Mathematical Analysis等, 担任编辑委员。

报告摘要:Let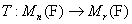 be a linear map between matrices (maybe of different sizes) over an arbitrary field 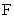. Many preserver problems can be formulated as the one preserving matrices annihilated by a fixed polynomial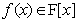, i.e.,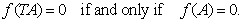For example, if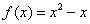, the above is equivalent to that 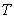preserves idempotent matrices; while if 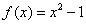, the above is equivalent to that 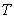preserves involution matrices. We find that when the domain 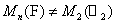, the zero set of 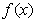is ``simple enough'' and 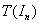is central in the range of 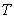, any such linear preserver 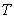assumes a canonical form, namely, 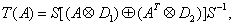for some invertible 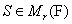, and diagonal matrices 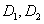of appropriate sizes. The diagonal entries of 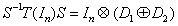satisfy the multiplier condition 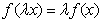. Here, by saying 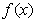is ``simple enough'' we mean that the zeroes of 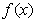does not form an additive coset of 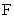. The result is indeed a consequence of our new finding that any disjoint idempotent preserver 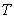assumes such a canonical form when the domain of 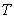is not .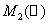