报告题目:The Turán number of Berge-K4 in 3-uniform Hypergraphs
报 告 人:康丽英教授 上海大学
照 片:

邀 请 人:李碧
报告时间:2020年11月10日(周二) 15:00-16:30
报告地点: 腾讯会议ID:338 410 643
报告人简介:康丽英,上海大学数学系教授,博士生导师。曾获“上海市三八红旗手”,“上海市曙光学者”称号。中国运筹学会常务理事、中国工业与应用数学学会组合图论专业委员会副主任委员、中国数学会组合图论分会理事。 担任国际期刊《Discrete Mathematics, Algorithms and Applications》、 《Journal of the Operations Research Society of China》、《Communications on Applied Mathematics and Computation》和国内期刊《运筹学学报》编委。 在《SIAM Discrete Mathematics 》、《Journal of Graph Theory》、《European Journal of Combinatorics》等学术期刊上发表学术论文140篇,主持完成5项国家自然科学基金项目。曾在美国南卡莱罗纳大学、荷兰蒂尔堡大学、法国巴黎十一大等多所大学进行学术访问和合作研究。
报告摘要:For a graph G = (V, E), a hypergraph H is called a Berge-G, if there is a bijection f : E(G) → E(H) such that e ⊆ f(e) for all e ∈ E(G). Denoted by B(G) the family of Berge-G hypergraphs. The maximum number of edges in an n-vertex r-graph with no subhypergraph isomorphic to any Berge-G is denoted by exr(n, B(G)). A recent result, due to Gerbner et al. (General lemmas for Berge-Turán hypergraph problems, European Journal of Combinatorics 86 (2020)), implies that for n ≥ 9, ex3(n, B(K4)) =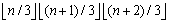 . In this talk we prove the remaining cases n = 7 and n = 8 for the completeness of the conclusion.
. In this talk we prove the remaining cases n = 7 and n = 8 for the completeness of the conclusion.